Stress

Stress

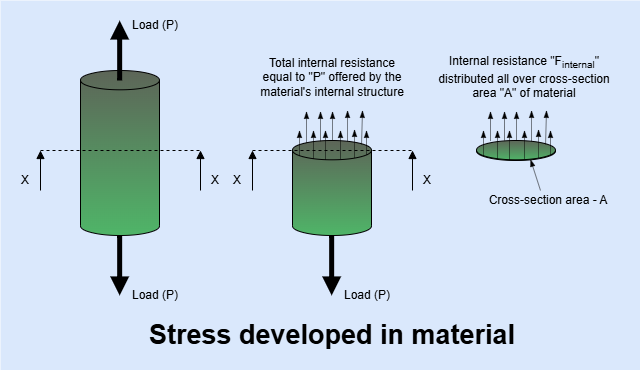
When an external force acts on a body, it tends to deform the body. To resist the deformation and maintain the equilibriem, internal resisting forces develop within the material. This internal resisting force per unit area is called stress.

Also, stress can be defined as the force intensity at a point, resisting separation or distortion of the material. It represents how the internal force is distributed through the material.

Stress is denoted by Greek letter sigma (\(\sigma\)).

Types of Stress

The major type of stresses we deal in engineering problems are as follow:

1. Normal Stress (\(\sigma\))

   • The stress where internal forces acts perpendicular to the surface of body.
   • Normal stress is denoted by (\(\sigma\))

   Normal Stress is further divided into two types:

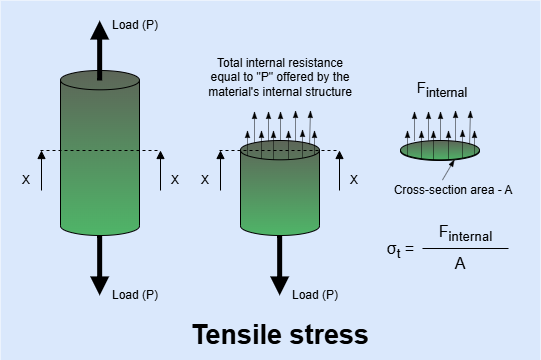
   1. Tensile Stress - A normal stress that tends to stretch or elongate the material.

      • Formula
        \[\sigma_{\text{t}} = \frac{F_{\text{internal}}}{A}\]
      • It is represented by a Positive (+) sign.
      • Example - Stress occured in crane cables
   

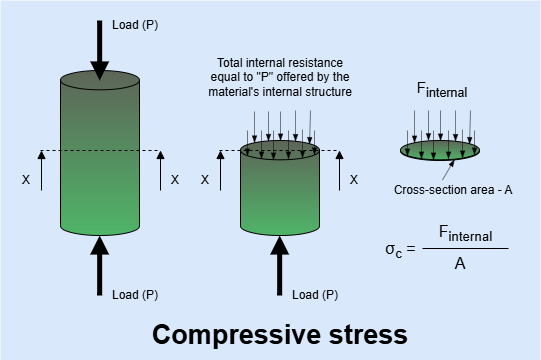
   2. Compressive Stress - A normal stress that tends to compress the material.

      • Formula
        \[\sigma_{\text{c}} = \frac{F_{\text{internal}}}{A}\]
      • It is represented by a Negative (-) sign.
      • Example - Stress occured in metro pillar due to load bearing.


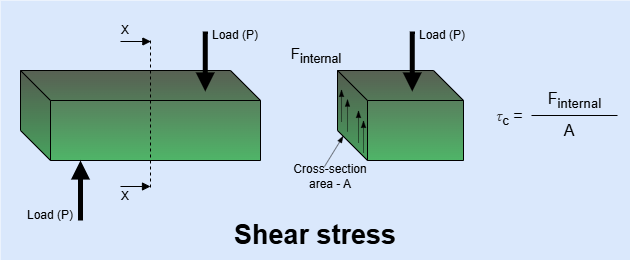
2. Shear Stress (\(\tau\))

   • The stress where internal forces acts parallel to the surface of body.
   • Formula
     \[\tau = \frac{F}{A}\]
   • Shear stress is denoted by (\(\tau\))
   • Example - Stress occured bolt joint.


3. Bending Stress (\(\sigma_{\text{b}}\))

   • Stress caused by loads that bend structural members, creating tension on one side and compression on the other.
   • Formula
     \[\sigma_{\text{b}} = \frac{My}{I}\]

   Where:

   • \(\sigma\) = Bending stress in \( Pa \) or \( MPa \)
   • \(M\) = Bending moment in \( N.m \)
   • \(y\) = Distance from neutral axis in \( m \)
   • \(I\) = Moment of inertia in \( m^4 \)
   • Bending stress is denoted by (\(\sigma_{\text{b}}\))
   • Example - Stress occured in cantilever beam.

4. Torsion Stress (\(\tau_{\text{max}}\))

   • Stress caused by loads that bend structural members, creating tension on one side and compression on the other.
   • Formula
     \[ \tau_{\text{max}} = \frac{Tr}{J}\]

   Where:

   • \(\tau_{\text{max}}\) = Maximum torsional shear stress in \( Pa \) or \( MPa \)
   • \(T\) = Applied torque in \( N.m \)
   • \(r\) = Radial distance from central axis in \( m \)
   • \(I\) = Polar moment of inertia in \( m^4 \)
   • Torsion stress is denoted by (\(\tau_{\text{max}}\))
   • Example - Stress occured in propellar shaft of vehicle.

5. Bearing Stress (\(\sigma_{\text{b}}\))

   • Bearing stress is a contact pressure between two separate bodies that occurs when one object presses against another. Unlike other stresses that develop within a material, bearing stress occurs at the interface between components.
   • Formula
     \[ \sigma_{\text{b}} = \frac{F}{A_b}\]

   Where:

   • \(\Sigma{\text{b}}\) = Bearing stress in \( Pa \) or \( MPa \)
   • \(F\) = Applied force in \( N.m \)
   • \(A_b\) = Projected bearing area in \( m^2 \)
   • Torsion stress is denoted by (\(\sigma_{\text{b}}\))
   • Example - Stress occured in between bolt and plate hole interface.

6. Thermal Stress (\(\sigma_{\text{th}}\))

   • Thermal stress develops when a material undergoes temperature changes but is constrained from expanding or contracting freely.
   • If material is freely allowed to expand and contract due to change in temperature, in that case thermal stress will not occur.
   • Formula
     \[\sigma_{th} = E \cdot \alpha \cdot \Delta T\]

   Where:

   • \(\alpha\) = Coefficient of thermal expansion in (\(1/^\circ\mathrm{C}\))
   • \(\Delta T\) = Temperature change (\(^\circ\mathrm{C}\))
   • \(E\) = Young's modulus \(Pa\)
   • Thermal stress is denoted by (\(\sigma_{\text{th}}\))
   • Example - Shatter of windsheild glass when cold water is poured on hot windsheild.